"Entropic gravity" TEIL 2: Das Holografische Prinzip

Hohle Welt (Quelle)

Leben wir auf der Innenseite einer Hohlkugel? Diese Frage mag einem in einem wissenschaftlichen orientierten Blog etwas komisch vorkommen. Es soll hier aber nicht um die Theorie der Hohlen Erde gehen, sondern um das holografische Prinzip. Die letzten Klarheiten zu dieser Frage, sollte verschwinden, nachdem wir in diesem Blogbeitrag eine Odyssee - vorbei am Ereignishorizonts eines Schwarzen Loches, durch die Gedankenwelten von Physikern, ab ins Nichts mit seiner Vakuumsenergie, durch einen Teilchenbeschleuniger mit winzigen schwarzen Löchern und auf einem (sehr flüssigen) Meer aus Quark-Gluonen-Plasma hin zum holografischen Prinzip - beendet haben. Möge die Irrfahrt beginnen ...








In TEIL I dieser Serie zur "entropic gravity", habe ich die Frage aufgeworfen, was Einsteins zerzauste Haare mit der Gravitation zu tun haben könnten. Um zu einer Antwort auf diese Frage und zur "entropic gravity" aus Erik Verlindes Publikation "On the Origin of Gravity and the Laws of Newton" zu kommen, habe ich zuerst versucht zu erklären, was Entropie überhaupt ist. Entropie zu verstehen reicht aber alleine nicht aus, denn Erik Verlinde setzt das holografische Prinzip voraus. In diesem Teil werden wir uns diesem widmen. Ich möchte dazu aber das holografische Prinzip nicht nur erklären, sondern auch rechtfertigen, warum es mehr als nur eine mathematische Spielerei (oder auch Spinnerei) ist. Gerade diese Rechtfertigung ist aber kein leichtes Unterfangen. Wer sich in dieser Odyssee hoffnungslos verloren sieht, braucht aber deswegen noch nicht aufgeben, denn auch ohne die Rechtfertigung zu verstehen, kann man den sicheren Hafen der "entropic gravity" erreichen. Gefesselt an einen Mast, lassen sich selbst "die Sirenen der Unverständlichkeit" überstehen.

1. Darstellung des Holografischen Prinzips

Illustration des Holografischen Prinzips
aus: Maldacena - The Illusion of Gravity

Kurz und knapp formuliert, besagt das holografische Prinzip, dass es zu einer Beschreibung von bestimmten Vorgängen in einem Raumgebiet eine äquivalente Beschreibung auf dessen Rand gibt. Anschaulich kann man sich das mit dieser Illustration auf der linken Seite klarmachen. Nach dem holografischen Prinzip kann man die Vorgänge des Jongleurs in der Kugel durch andere Vorgänge auf der Oberfläche dieser Kugel beschreiben. Das hört sich erst einmal nicht sehr spektulär an, aber diese Vorgänge in der Kugel gehorchen dabei der Gravitation, während auf der Oberfläche die selben Vorgänge der Quantenmechanik gehorchen. Die Namensgebung ist dabei am Hologramm orientiert. Ein Hologramm ist selber flach, vermittelt aber den Eindruck eines räumlichen Bildes.


Etwas genauer: Es könnte sein, dass sich alles was wir erleben eigentlich nur auf dem flachen zweidimensionalen "Rand" des Universums abspielt und die drei Dimensionen und die Gravitation nur eine Illusion ist, die - wie beim Hologramm - entsteht. Diese Beschreibung ist nun auch noch etwas ungenau. Eigentlich muss man von 3 und 4 Dimensionen sprechen, da Zeit und Raum eng miteinander verflochten sind. Außerdem ist "Rand" auch eine sehr unpassende Formulierung, da es hier nicht um einen Rand, im Sinne einer Grenze am Ende des Universums handelt. Um der Anschauung willen, kann man es sich aber schon wie den Rand (also die Oberfläche) einer Kugel vorstellen. Dabei sind diese Vorgänge auf dem "Rand" aber nicht etwa nur eine Abbild, wie eine Film, der auf dem Rand abläuft, sondern eine Art Code. Wie bei einer Computersoftware (oder auch im Film Matrix) ist dieser Code aus Bits, also aus $0$ und $1$ aufgebaut. Das hat damit zu tun, dass sich dieser Rand nicht beliebig klein unterteilen lässt. Es gibt also eine minimale Größe und diese Größe ist Information in Bits.


Die ganze Idee hat mit der Stringtheorie zu tun und wie die Stringtheorie sieht das erst einmal nach einer Spinnerei aus.

Stringtheorie: Nur ein Idee? (Quelle: xkcd.com)

2. Erklärung des Holografischen Prinzips

Wie kommt man auf eine solche Idee wie das holografische Prinzip? Um diese Frage zu klären muss ich sehr weit ausholen. In der heutigen Physik gibt es zwei wichtige Theorien: Die Quantenmechanik und die Relavitätstheorie (Wenn ich von Quantenmechanik spreche meine ich immer das Standardmodell, das ist die Weiterentwickelung der ursprünglichen Quantenmechanik) . Beide Theorien würden x-mal experimentell bestätigt. Jeder Versuch diese Theorien zu falsifizieren ist bisher gescheitert und die Theorien wurden mal um mal bestätigt. Einstein etwa wollte mit einem Gedankenexperiment zeigen, dass mit der Quantenmechanik etwas nicht ganz stimmen kann (vgl. EPR-Effekt bzw Quantenverschränkung). Dabei solle es nach Einstein eine spukhafte Fernwirkung geben, die nicht sein könne. Es blieb aber nicht bei einem Gedankenexperiment und diese spukhafte Fernwirkung konnte in der Tat nachgewiesen werden. Aber nicht nur das, die spukhafte Fernwirkung wird sogar schon ganz praktisch in der Quantenkryptografie eingesetzt (vgl. Spon.de). Auf der anderen Seite sind Atomkraftwerke, Atombomben und GPS experimentelle Belege für die Relativitätstheorie. Es gibt nur ein Problem, beide Theorien passen irgendwie nicht zusammen. In der allgemeine Relativitätstheorie (ab jetzt durch ART abgekürzt) kann man den Raum etwa beliebig klein unterteilen, während es in der Quantenmechanik (fortan QM) eine Minimum für diese Unterteilung gibt. In der ART ist der Raum quasi "glatt" während er in der "QM" eher einer Art Gitter, das sich nicht weiter unterteilen lässt. Derartige Unterschiede sind nun zwar keine Widersprüche im eigentlichen Sinn. Widersprüche treten erst dann auf, wenn man die Theorien versucht zu verbinden. Die Kräfte in der QM sind gequantelt, sind also Teilchen (Bosonen) während die Gravitation in der ART eine Eigenschaft des Raums und der Zeit ist. Versucht man nun die Gravitation zu quanteln, also auch zu einem Austauschteilchen wie die Bosonen zu machen, beginnen die Widersprüche und es stimmt hinten und vorne nicht mehr.


In der Praxis ist es für Vorhersagen erst einmal kein Problem zwei verschiedene Theorien zu haben, da die QM mikroskopische Vorgänge auf Atomebene beschreibt, während die ART makroskopische Vorgänge wie das Fallen eines Apfels oder die Planetenbahnen beschreibt. Betrachtet man etwa Staubkörner in einem Lichtkegel einer Lampe, scheinen diese ganz unbekümmert von der der Erdanziehung umher zu fliegen. Noch kleinere Teilchen sind noch "unbekümmerter". Die Erdanziehung ist schlicht zu gering um einen Effekt zu haben. Das sich diese Theorien nicht in die Quere kommen ist es aber dann ein Problem, wenn es darum geht eine vereinheitlichte Theorie zu bekommen, denn man kann das Wechselspiel beider Theorien fast nicht beobachten. Man würde also eine Situation brauchen, in der die Gravitation so stark wirkt, dass sie große Auswirkung auf die Quantenwelt hat. Eine derartige Situation findet man glücklicherweise in der Nähe eines schwarzen Loches. Diese eigenen sich zwar (noch?!) nicht für experimentelle Untersuchungen, aber immerhin für theoretische...

2.1 Thermodynamik Schwarzer Löcher

"Raumzeitkrümmung"
(Quelle: icanhascheezburger.com)

Wie schon diese Artikelserie fängt der Weg zum holografischen Prinzip bei der Entropie an, bei der Entropie und schwarzen Löchern. Bevor wir aber zu beiden kommen, noch eine kurze Erklärung zur Raumzeitkrümmung. In der ART ist die Gravitation eine Eigenschaft des Raumes und der Zeit. Massen ziehen sich deshalb an, weil die Raumzeit gekrümmt wird. Diese Krümmung können wir uns nicht vorstellen, da die Raumzeit 4 dimensional (3 Raumrichtungen 1 Zeitrichtung) ist. Daher greift man häufig auf eine 2 dimensionale Erklärung zurück. Wenn man etwa eine Kugel auf ein ausgespanntes Bettlaken legt, dann krümmt sich dieses. Lässt man nun eine zweite Kugel auf diese Ausbeulung des Bettlakens rollen, dann würde die Bahn abgelenkt werden.

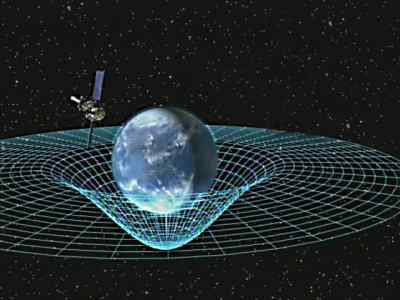Raumzeitkrümmung
(Quelle: plus.maths.org)

Bei der Gravitation verhält es sich analog (vgl. die NASA Illustration links). Neben der Anzahl der Dimension gibt es aber noch einen Unterschied. Würde man eine Kugel so im Bettlaken anschieben, dass sie in einer Bahn um die andere Kugel kreist, würde die Reibung diese Kugel immer mehr abbremsen. Im Vakuum gibt es aber keine Reibung, so dass etwa ein Satellit auf seiner Kreisbahn bleiben müsste. Lichtteilchen, also Photonen, haben keine Masse und würden nach Newton somit auch nicht von Masse angezogen werden. Wenn aber die Raumzeit selber gekrümmt ist, dann wird dadurch auch ein gerader Lichtstrahl gekrümmt. Licht wird also nicht von der geraden Bahn abgelenkt, sondern die gerade Bahn selber wird "krumm". Für die grundlegende Idee eines schwarzes Loches müssen wir aber noch nicht einmal die ART bemühen. Die Idee zu schwarzen Löchern oder schwarzen Sterne ist über hundert Jahre älter als Einsteins Theorie.

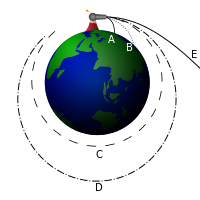Kosmische Geschwindigkeiten
(Quelle: wiki)

Dazu werfen wir einen Blick auf die Fluchtgeschwindigkeit. Hierzu ist die Grafik rechts hilfreich. Wenn man eine Kanonenkugel abschießt (oder allgemein einen Körper auf eine bestimmte Geschwindigkeit beschleunigt) dann wird sie bei "geringere" Geschwindigkeit, wie bei A oder B zurück auf die Erde fallen. Erreicht die Geschwindigkeit einen bestimmten Wert - die 1. kosmische Geschwindigkeit - dann würde die Kanonenkugel in einer runden Bahn um die Erde "herum fallen" wie in C dargestellt (Reibung vernachlässigt). Ist die Geschwindigkeit etwas höher, dann wird die Bahn elliptisch, wie bei D. Erreicht die Geschwindigkeit den Wert der Fluchtgeschwindigkeit - auch 2. kosmische Geschwindigkeit genannt - wie bei E, dann entfernt sich der Körper dauerhaft von der Erde. Diese Werte hängen von der Masse der Erde ab, die Masse des Körpers kürzt sich dabei raus und ist irrelevant. Bereits im 18 Jahrhundert gab es dann die Überlegung von "schwarzen Sternen". Wenn die Geschwindigkeit des Lichts geringer als die Fluchtgeschwindigkeit eines solchen Sternes ist, dann würde das Licht immer wieder auf den Stern "zurückfallen". Man würde also einen solchen Stern nicht leuchten sehen. Es gibt aber hier zur ART noch einen entscheidenden Unterschied. Wenn Licht keine Masse hat (was man damals noch nicht wusste) würde man beim berechnen der Fluchtgeschwindigkeit beim herauskürzen der Masse durch 0 teilen. Für masselose Teilchen wie Licht würde die Fluchtgeschwindigkeit gegen unendlich gehen. In der ART ist die Gravitation aber eine Eigenschaft des Raumes und gilt somit auch für masselose Teilchen wie Photonen (Photonoen sind die Lichteilchen). Das Schema ist aber dennoch das Gleiche. Bei einem schwarzen Loch ist nun die Fluchtgeschwindigkeit höher als die Lichtgeschwindigkeit. Da nichts schneller als die Lichtgeschwindigkeit sein kann (auch nicht Neutrinos) kann einem schwarzen Loch nichts entkommen.


Dies bringt uns nun zur Entropie und einem Problem mit den Schwarzen Löchern. John Archibald Wheeler, der auch den Begriff "schwarze Löcher" prägte, fiel dieses Problem als erstes auf. Sterne wie unsere Sonne geben Wärme durch Photonen (also Licht ab). Wenn man nun aber etwa ein heißes Gas oder sonst etwas mit Entropie in einem schwarzen Loch versenkt, dann verschwindet es auf nimmer Wiedersehen. Das schwarze Loch strahlt nichts mehr ab. Das würde aber heißen, dass die Entropie im Universum abnimmt. Entropie kann aber nur dann abnehmen, wenn sie woanders zunimmt, einfach verschwinden kann sie nicht. Die Energie ist zwar noch erhalten, weil die Masse des schwarzen Loches zunimmt (und Energie und Masse nach $E=mc^2$ äquivalent ist), aber weil das schwarze Loch keine Wärme/Energie abstrahlen kann, wäre die Entropie des hereinfallenden Körpers unweigerlich verloren. Der zweite Hauptsatz der Thermodynamik wäre verletzt, ... außer aber, das schwarze Loch hätte eine Entropie, das passt aber nicht mit der fehlenden Wärme zusammen...


Im Jahr 1971 veröffentlichte Stephen Hawking die Arbeit "Gravitational Radiation from Colliding Black Holes". Dabei stellte er fest, dass der Ereignishorizont (das ist der Bereich ab dem nichts mehr entkommen kann) eines schwarzen Loches niemals abnehmen kann (Christodoulou zeigte dies unabhängig und Speziallfälle wurden schon davor gezeigt - aber nicht allgemein bewiesen). "Niemals abnehmen kann"? Das kommt einem doch von der Entropie bekannt vor. Und genau das dachte sich dann auch Jacob Bekenstein der damals bei Wheeler promovierte.


Auf den ersten Blick ist diese Analogie aber doch etwas plump. Nur weil die Entropie nicht abnehmen und der Ereignishorizonts eines Schwarzen Loches nicht kleiner werden kann, muss das doch noch nichts miteinander zu tun haben. Hier ist es nun wichtig, was ich im ersten Teil über die Entropie geschrieben habe. Ich habe versucht die Zusammenhänge der thermodynamischen Entropie mit der Shannonentropie klar zu machen und diese Zusammenhänge spielen nun eine Rolle. Die Entropie in der Thermodynamik ist durch makroskopische Parameter gegeben und man kann die Entropie auch als die Ungewissheit verstehen, die ich - bei gegebenen makroskopischen Parametern - über den Mikroskopischen Zustand habe. Wenn nun irgendwas in einem schwarzen Loch versenke, dann ist meine Ungewissheit so gesehen nicht verschwunden, dafür sind aber die thermodynamischen Parameter "verschwunden" durch die ich die Ungewissheit bestimmt habe. Dafür habe ich aber eine neue Größe, nämlich die Größe des Ereignishorizonts. Die Ungewissheit an Information ist aber nicht nur eine abstrakte Größe sondern entspricht der wirklichen Information die auf mikroskopischer Ebene vorhanden ist. Beim Überqueren des Ereignishorizonts wird dann diese Information (für einen äußeren Beobachter) quasi gelöscht und man hat nur noch die Größe des Ereignishorizonts. Gerade dieses löschen der Information wird später noch eine Rolle spielen. Im Moment ist es wichtiger, dass sich unsere Ungewissheit nicht geändert hat und wir statt den thermodynamischen Parametern für die Bestimmung der Ungewissheit nun die Oberfläche des Ereignishorizonts als einen möglichen Parameter für die Bestimmung haben. Betrachtet man es aus dieser Sicht, erscheint diese Analogie zumindest etwas stimmiger. Diesem Argumentationsschema folgte auch Bekenstein in seiner Publikation "Black Holes and Entropy" (Wer Teil I der Serie verstanden hat, dürfte Section III der Publikation halbwegs folgen können). Damit hat man zumindest mal einen stimmigen Ansatz, für einen möglichen Zusammenhang. Die Details von Bekensteins Herleitung lassen wir mal beiseite und nehmen einfach mal hin, dass ein schwarzes Loch eine Entropie $S_{BH}$ hat die von der Oberfläche des Ereignishorizonts abhängt (das BH im Index von S steht für "black hole"). Wenn nun ein schwarzes Loch eine Entropie hat, dann kann man nun den zweiten Hauptsatz der Thermodynamik verallgemeinern:

"Die (thermodynamisch) Entropie und die Summe der Oberflächen aller Ereignishorizonte kann in einem abgeschlossenen System niemals abnehmen."

Oder schlicht $S + S_{BH} > 0$. Außerdem könnte man mit dieser Entropie nun wie in der Thermodynamik rechnen und etwa die Temperatur eines schwarzen Loches bestimmen, denn es gilt:

$${\rm d}S = \frac{\delta Q}{T}$$

$Q$ bezeichnet hierbei die Wärme. Wärme ist aber nichts anderes als Energie und Energie ist nach $E=mc^2$ nichts anderes als Masse. Mithilfe der Masse und der Entropie könnte man nun also die Temperatur bestimmen. Das ist aber blöd, denn ein schwarzes Loch hat ja eigentlich irgendwie doch keine Temperatur. Bekenstein selber schreibt nach Bestimmung der Temperatur "but we should emphasize that one should not regard $T_{bh}$ as the temperature of the black hole; such an identification can lead to paradoxes ..." (Quelle: s.o.). Es wäre nämlich paradox, wenn das die "echte" Temperatur wäre, denn was eine Temperatur hat, strahlt auch was ab und ein schwarzes Loch strahlt ja nichts ab.... oder etwa doch?!

2.2 Hawking-Strahlung

Wir verlassen Bekensteins Gedankenwelt erst einmal und kommen noch einmal zu Stephen Hawking. Dieser war von Bekensteins Überlegungen, dass ein schwarzes Loch eine Entropie haben müsse, zuerst nicht wirklich überzeugt. Das änderte sich aber, als er auf die Hawking-strahlung kam. Die Thermodynamik soll uns nun erst einmal nicht weiter kümmern und wir widmen uns ganz Nullpunktsenergie des Vakuums, der Vakuumenergie. So wie es beim holografischen Prinzip nicht um die pseudowissenschaftliche Hohle Welt gehen soll, so geht es auch hier nicht um irgendwelche pseudowissenschaftlichen Technologie die uns seit Jahren vorenthalten wird, sondern um den aktuellen wissenschaftlichen Kenntnisstand (eine mögliche Nutzung dieser Energie ist nicht gänzlich auszuschließen aber nach aktuellem Kenntnisstand nicht möglich. Siehe dazu etwa diese Studie der NASA. Eine Rakete die nach 10 Jahren Beschleunigung gerade mal eine Geschwindigkeit von 0,1 m/s erreicht, ist fürn A.....).


Was ist diese Vakuumsenergie? Nun in der Quantenmechanik ist alles ein wenig unscharf und selbst wenn nichts da ist, ist es nicht so ganz "Nichts". Selbst bei kompletter Abwesenheit von Teilchen, gibt es kleine Fluktuationen im "Nichts"


Fluktuation im Nichts? Geht es auch genauer. Ja, und dazu begeben wir uns zur Geburtstunde der Quantenmechanik ins Jahr 1900 zurück, als Max Planck sein Strahlungsgesetz in seinem Vortrag "Zur Theorie des Gesetzes der Energieverteilung im Normalspectrum" formulierte.

Glühendes Metall (Quelle: wiki)

Legt man einen schwarzen und einen weißen Gegenstand in die Sonne, dann wird der schwarze Gegenstand stärker aufgeheizt als der weiße. Dies hat schlicht was mit der Eigenschaft eines Stoffes elektromagnetische Strahlung (also auch Licht) zu absorbieren. Auf der anderen Seite geben erhitze Gegenstände elektromagnetische Strahlung in verschieden Spektren ab. Ein Beispiel wäre etwa ein glühendes Metal, das in einer bestimmten Farbe leuchtet. Hat man nun einen Körper mit einer perfekten Absorption spricht man von einem Schwarzen Körper (vollkommenes Absorbationsvermögen ist praktisch nicht möglich, aber etwa Metallen verhalten sich annähernd so).

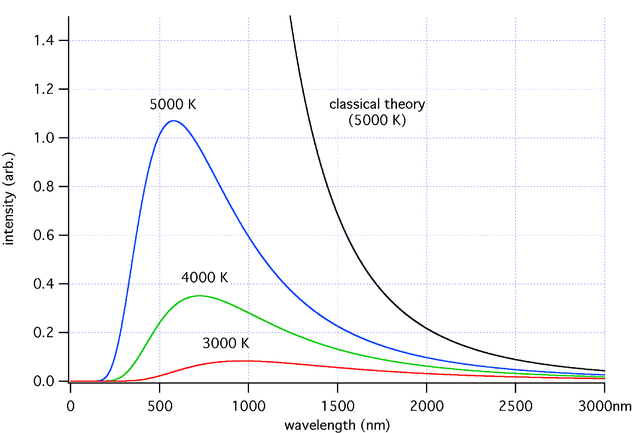Spektrum eines schwarzen Körpers
(Quelle: wiki)

Berechnet man nun mit der klassischen Physik diese Strahlung eines solchen schwarzen Körpers passiert etwas komisches. Für immer kleinere Wellenlängen geht die Intensität gegen unendlich (vgl. schwarze Kurve auf dem linken Schaubild). Die Sonne verhält sich annähernd wie ein schwarzer Körper und klassisch würde das heißen, dass die Sonne alles vernichtende Gammastrahlung (elektromagnetische Strahlung niedrieger Wellenlänge) von unvorstellbarer Intensität aussenden würde. Ich sitze hier aber (ziemlich) unverstrahlt und die klassische Theorie kann deshalb nicht stimmen.



Die gemessenen Intensitäten der elektromagnetischen Strahlung der Sonne verhält sich ziemlich genau wie blaue Kurve in dem Schaubild und diese Kurve entspricht Plancks Strahlungsgesetz. Um auf dieses Gesetz zu kommen, nahm Planck an, dass elektromagnetische Strahlung Energie nur in diskreten (also genau bestimmten) Mengen austauschen kann. Diese Idee entwickelte Einstein in seiner Arbeit "Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt" weiter und nahm an, dass die elektromagnetische Kraft in kleinen Paketen (oder Quanten) vorkommt. Die Pakete oder Quanten elektromagnetischer Strahlung bezeichnet man heute als Photonen. Einstein bekam später für diese Arbeit den Nobelpreis (und nicht für die Relativitätstheorie wie viele meinen).


Es soll uns aber für die Nullpunktsenergie nicht diese Arbeit von Einstein interessieren, sondern eine spätere Untersuchung, die er gemeinsam mit Otto Stern zum Planckschen Strahlungsgesetz machte: "Einige Argumente für die Annahme einer molekularen Agitation beim absoluten Nullpunkt".

Abweichung durch Nullpunktsenergie
(Quelle: s.o.)

Einstein und Stern untersuchten dabei experiemtelle Ergnisse zur spezifische Wärmekapazität von Wasserstoff bei niedrigen Temperaturen und stellten dabei eine Abweichung von Plancks Gesetz um $\frac{h\nu}{2}$ fest. Während Kurve II den theoretischen Werten von Plancks Gesetz entspricht, entspricht die Kurve I den theoretischen Werten, wenn man zu Plancks Gesetz den Term $\frac{h\nu}{2}$ hinzu addiert. Die experimentellen Werte sind durch Kreuze angegeben und stimmen sehr gut mit Kurve I überein.



Dieses Phänomen war vorerst unverstanden und wurde erst klarer durch Heisenbergs Unschärferelation. Durch die Unschärferelation ergibt sich, dass der Grundzustand eines Teilchens, der Zustand geringstmöglicher Energie, nicht exakt bestimmt ist und der von Einstein und Stern aus Experimenten bestimmte Wert taucht beim Errechnen von alleine auf.


Diese Nullpunktenergie hat nun unter anderem zur Folge, dass Helium selbst am absoluten Temperaturnullpunkt $0~{\rm K}$ (und bei Normaldruck) nicht fest wird, sondern flüssig bleiben sollte. Da sich der absolute Nullpunkt nicht erreichen lässt (3. Hauptsatz der Thermodynamik), kann man dies nicht experimentell belegen, aber selbst bei sehr nahen Annäherung an den Nullpunkt, verhält sich Helium wie eine Flüssigkeit. Darüber hinaus hat diese Flüssigkeit noch faszinierende Eigenschaften (siehe Suprafluidität). Einen eindeutigen experimentellen Beleg für die Vakuumenergie gibt es bis dato nicht. So kann etwa der Casimir-effekt, der üblicherweise durch die Vakuumenergie erklärt wird, auch auf andere Weise erklärt werden und man kann ihn somit nicht konsequent als Beleg werten und wir bewegen uns im Moment somit auf rein theoretischem Terrain. Dennoch sprechen die Indizien sehr sehr deutlich für die Existenz der Vakuumenergie.


Diese Vakuumenergie führt uns nun auch zur Hawking-Strahlung aus Hawkings Publikation "Particle creation by black holes" .Die Vakuumenergie kann man sich auch als spontan entstehende Paare von virtuelle Teilchen vorstellen. Ganz spontan aus dem nichts entsteht ein Teilchen und ein Antiteilchen die ganz kurz auseinanderfliegen und sich dann gegenseitig wieder auslöschen. Hawking hat nun überlegt, was denn ganz nahe am Ereignishorizont mit solchen Teilchenpaaren passieren könnte.

Hawking-strahlung
(Quelle: newscientist.com)

Ereignet sich diese Entstehung von Teilchen und Antiteilchen nahe am Horizont eines Schwarzen Loches, so kann es sein, dass ein Teilchen vom schwarzen Loch eingefangen wird, während das andere weiter fliegt. In einem solchen Fall würde dieses äußere Teilchen nun "real" werden. Das andere Teilchen hätte aus der Sicht eines äußeren Beobachters dann eine negative Energie und würde somit die Masse (Äquivalent zur Energie) des Schwarzen Lochs verringern.





kurzer Einschub: Vakuumenergie, negative Energie, virtuelle Teilchen - das sind doch alles nur theoretische Spinnereien. In der Tat ist das alles nur mal theoretisch und wirkt von unserem "gesunden Menschenverstand" aus vollkommen unwirklich. Nach der Erfindung der Lokomotive, argumentierten einige auch mit "gesundem Menschenverstand", dass die hohen Geschwindigkeiten (30 km/h) zu einem zersetzen der Organe führen würde, obwohl das Relativitätsprinzip schon seit Galilei bekannt war.

Was von der bloßen Vorstellung zu halten ist, hat wohl nie jemand besser als Hegel mit folgenden Worten formuliert:

"Das Tiefe, das der Geist von innen heraus, aber nur bis in sein vorstellendes Bewußtsein treibt und es in diesem stehenläßt, – und die Unwissenheit dieses Bewußtseins, was das ist, was es sagt, ist dieselbe Verknüpfung des Hohen und Niedrigen, welche an dem Lebendigen die Natur in der Verknüpfung des Organs seiner höchsten Vollendung, des Organs der Zeugung, und des Organs des Pissens naiv ausdrückt. – Das unendliche Urteil als unendliches wäre die Vollendung des sich selbst erfassenden Lebens; das in der Vorstellung bleibende Bewußtsein desselben aber verhält sich als Pissen."
(Quelle: G.W.F. Hegel - "Die Phänomenologie des Geistes" , Werkausgabe S. 262, fett bei Hegel kursiv)

Gehen wir einfach mal davon aus, dass sich die Wirklichkeit nicht nach unseren Vorstellungen richtet und der "gesunde Menschenverstand" nichts "natürliches", sondern eine kulturelle, sich mit der Zeit ändernde, Erscheinung ist. Und akzeptieren wir darüber hinaus den Fakt, dass Theorien in der Geschichte der Wissenschaft, häufig ein mächtiges Werkzeug waren. Lassen wir die Sirenen der Unverständlichkeit weiter singen und unsere Vorstellungen bezirzen und lassen die Einsicht, dass unser Geist mehr vermag als bloßes Vorstellen, unsere Fesseln sein, die uns auf der Odyssee vor den Sirenen bewahren.

Halten die Fesseln? Gut, weiter gehts:



Was bedeutet nun diese Überlegung von Hawking. In aller erster Linie widerspricht sie dem zuvor gefunden Gesetz von Hawking, dass der Horizont immer größer werden muss. Wenn nämlich ein Teilchen entkommt und das andere Teilchen die Masse des schwarzen Loches reduziert, dann wird wegen der geringeren Masse auch der Ereignishorizont kleiner. Hawking hatte bei der früheren Arbeit nur die ART berücksichtigt, wenn aber die QM dazukommt, dann gilt das nicht mehr, ABER, wenn der Horizont abnimmt, wird gleichzeitig Wärme durch das wegfliegende Teilchen abgeben. Dadurch wird aber die thermodynamische Entropie wieder erhöht. Somit gilt der verallgemeinerte zweite Hauptsatz der Thermodynamik immer noch, denn $S + S_{\rm BH} zusammen bleiben größer als null. Wenn die Thermodynamische Entropie abnimmt, dann nimmt der Horizont zu, wenn der Horizont abnimmt, dann nimmt die Thermodynamische Entropie zu.

Außerdem scheint nun das schwarze Loch sich exakt wie ein schwarzer Körper vom Planckschen Strahlungsgesetz. Es hat eine Temperatur (die nun ganz und garnicht mehr paradox ist wie bei Bekenstein) und strahlt elektromagnetische Strahlung ab.

Ich habe geschrieben, dass es so so scheint. Das hat damit zu tun, dass diese Strahlung ja nicht wirklich vom schwarzen Loch kommt, sondern von den virtuellen Teilchen. Lässt man aber mal die Erklärung von Hawking, wie diese Strahlung zustande kommt, dann verhält sich das schwarze Loch genau so wie man es aus Sicht der Thermodynamik und dem Plankschen Strahlungsgesetz erwarten würde.

Das ist ein durchaus faszinierendes Ergebnis. Hawking nutzt Vorhersagen aus ART und QM, den beiden Theorie die eigentlich nicht so Recht zusammen passen wollen, und was dabei heraus kommt ist ein zu Strahlensatz und Thermodynamik stimmiges Bild. Dies legt nahe, dass es hier tief verwurzelte Zusammenhänge gibt und ist motivierend hier weiter zu "bohren". Denn es könnte eine Theorie geben die ART und QM quasi als Speziallfälle enthält und bei dieser Theorie erscheint es nicht nur so, als ob das schwarze Loch strahlt wie man es erwarten würde, sonder, dass es wirklich strahlt. Und es gibt auch schon eine gute Stelle an der man weiter (theoretisch) untersuchen kann was hier vorgeht...

2.3 Das Informationsparadoxon

Bekenstein hat bei seinen Arbeiten zur Thermodynamik schwarzer Löcher das Verschwinden von Information am Ereignishorizont betrachtet. Ich sprach davon das diese Information "gelöscht" wird. Von außen betrachtet ist diese Sichtweise erst einmal kein Problem, denn für jemand außerhalb des Ereignishorizonts ist diese Information unweigerlich verloren. Vom schwarzen Loch kennt man nur noch die Masse, den Drehimpuls (Rotation) und die Ladung (man sagt auch ein schwarzes Loch hat keine Haare). Wenn auch die Information für einen Beobachter außerhalb unweigerlich verloren ist, so kann Sie aber innerhalb des schwarzen Loches durchaus immer noch vorhanden sein. Wenn das Loch aber - nach Hawkings Theorie - strahlen (und in einigen Fällen auch zerstrahlen) kann, ist das ein Problem. Warum?

Nun die Strahlung kommt von den virtuellen Teilchen und haben ja nichts mit dem inneren des schwarzen Lochs am Hut. Wenn ich ein weißes Kaninchen in einen schwarzen Zylinder stecke und eine weiße Taube fliegt raus und im selben Moment verpufft der Zylinder, dann ist da irgendwas faul. ( ... and if you go chasing rabits, and you know you gonna fall ...)


ART und QM haben gemeinsam sehr interessante Vorhersagen produziert, nun taucht aber doch ein Widerspruch auf. Information geht rein, kommt aber beim zerstrahlen nicht mehr raus. Um genau zu sein widerspricht dies der Unitarität der QM. Man braucht dazu nicht verstehen, was Unitarität ist, zur Anschauung reicht das Beispiel mit dem Kaninchen, das mitsamt dem Zylinder auf nimmer wiedersehen verschwindet.


Hawking selbst, war der Meinung, dass die Information wirklich verloren ist. Dann müsste man die Quantenmechanik verändern. Andere haben dem teils energisch widersprochen. Die Position lassen sich zumeist den Spezialisierungsbereichen zuordnen. Während die "Relativitätstheoretiker" eher an der QM "rum basteln" wollten, wollten die "Quantenmechaniker" eher an der ART "rum basteln". Zu denen die Hawking energisch widersprochen haben, gehörten unter anderem Gerardus 't Hooft und Leonard Susskind. Susskind hat seinen "Krieg" mit Hawking auch in einem Buch beschrieben (siehe rechts). Und mit Susskind und 't Hooft kommen wir nun endlich auch zum holografischen Prinzip.



Betrachten wir dazu zuerst einmal die Grundlegende Idee von 't Hooft in der Publikation: "Black Hole Evaporation without Information Loss". Die Idee ist, dass ein Teilchen, das den Ereignishorizont passiert, diesen so beeinflusst, dass die Information erhalten bleibt. Ein Teilchen hat ja eine Energie und jede Energie (weil Äquivalent mit Masse) erzeugt eine Raumkrümmung und dies Raumkrümmung beeinflusst dabei die Raumkrümmung am Ereignishorizont. Dadurch soll die Information auf dem Ereignishorizont erhalten bleiben. Schematisch kann man das sich vorstellen, wie einen Stein den man in Wasser wirft. Die Wellen die dabei erzeugt werden hängen ab vom Gewicht des Steines und der Geschwindigkeit mit der man den Stein hineinwirft ab (also vom Impuls der Masse mal Geschwindigkeit ist). Diese Wellen enthalten somit quasi die Information über den Impuls. Vergleichbar sollen auf diese Weise die Information eines Quantenmechanischen Zustands durch den Ereignishorizont erhalten bleiben. Das wiederum soll dann einen Einfluss auf die Teilchen haben, die nach Hawkings Theorie ausgesendet werden. Es würde zwar immer noch ein "anderes" Teilchen wegfliegen (anderes Teilchen lässt sich in der QM nicht wirklich sagen - aber das ist ein Thema für sich), dieses hätte aber genau den selben Zustand, wie das Teilchen das hineingefallen ist. In der obigen Publikation wird das aber mathematisch nur in einem vereinfachten Modell gezeigt.


Nun ist aber das Informatiosnparadoxon nicht die einzige Motivation für die Entwicklung des holografischen Prinzip. Wir hatten bei Bekenstein bereits den Zusammenhang der Oberfläche eines schwarzen Loches mit der Entropie. In der Thermodynamik ist aber das Volumen eine relevante Größe. Betrachtet man etwa ein Raster auf einer Fläche, etwa ein kariertes Papier. Wenn man nun in jedem Kästchen ein Bit Information reinschreiben kann (also 0 oder 1) dann könnte ich bei 10 auf 10 Kästchen insgesamt $10 \cdot 10 = 100$ Bit Information eintragen. Nehme ich dagegen ein Gitter in einem Volumen dann könnte darin $10 \cdot 10 \cdot 10 = 1000$ Bit Information eintragen. Wenn sich eine Fläche nicht beliebig klein unterteilen lässt, dann kann ich dort nur eine, durch die Fläche begrenzte, Menge an Information unterbringen. Diese Begrenzung nennt sich Bekenstein-Grenze und 't Hooft hat sich damit unter anderem in der Arbeit "Dimensional Reduction in Quantum Gravity" auseinandergesetzt. Es wäre möglich, dass es eine Begrenzung der Freiheitsgrade in einem Volumen durch die umschließende Fläche gibt (die Freiheitsgrade in einem System mit 2 Zuständen, wie beim Münzwurf, wäre Exakt die Entropie in Bit). Diese Begrenzung ist aber riesig und würde in der Thermodynamik gar nicht auffallen. Warum die Fläche übrigens nicht beliebig klein unterteilt werden kann lassen wir mal beiseite. Das hat was mit der Planck-Fläche zu tun und 't Hooft schreibt in dieser Arbeit: "nature is much more crazy at the Planck scale than even string theorists could have imagined." und das heißt was, denn Stringtheorie ist schon ziemlich "verrückt".


Wenn sich diese Idee bewahrheiten sollte, wäre das ein mehr als faszinierendes Ergebnis. Bei Hawking gab es noch ein sehr stimmiges Wechselspiel zwischen ART und QM. Bei 't Hooft ist das aber schon viel mehr. Wenn Teilchen, die sich nach der QM verhalten, Eigenschaften auf den Ereignishorizont eines Schwarzen Loches, das sich nach der ART verhält, übertragen kann, dann sind die Theorien nicht nur stimmig zu einander, sondern in Teilaspekten sogar identisch, nur eben in anderen Dimensionen (einmal flach - einmal 3D). QM und ART erscheinen nicht nur stimmig zueinander, sie lassen sich verknüpfen. Dazu müsste aber das holografische Prinzip bewiesen werden.

Auf die Arbeiten von t' Hooft folgten dann noch Arbeiten von Susskind (der selber schon in diese Richtung ging) wie etwa "The World as a Hologram" die diese Idee im Rahmen der Stringtheorie noch etwas präzisierte. Im Jahr 1999 veröffentlichte dann Juan Maldacena eine Publikation die Einschlug wie eine Bombe ...

2.4 AdS/CFT Korrespondenz

Die Publikation unter dem Titel "The Large N Limit of Superconformal Field Theories and Supergravity" hat für einen Laien erst einmal einen nichts sagenden Titel und auch wenn man als Laie das "abstract" liest, dürfte man keinen blassen Schimmer haben worüber es geht. Dass es sich aber um eine Arbeit von immenser Bedeutung handelt, dürfte jedem klar werden wenn man die Zititationszahl sieht. Die Arbeit wurde mittlerweile fast 10000 mal zitiert!!!

Maldacena bewieß darin die Dualität einer Typ IIB Stringtheorie in einem 5 dimensionalen Anti-de-Sitter Raum ($AdS_5 × S^5$) mit einer supersymmetrischen N=4 Yang-Mills Eichtheorie auf dem 4 dimensionalen Rand des $AdS_5$. Faszinierend oder?

Zwei Ebenen schneiden sich in
einer Geraden (wiki)

Nicht verstanden? Ok, Klartext: Erstmal zum Anti-de-Sitter Raum. Wenn man eine Funktion hat, dann kann man etwa den Schnittpunkt mit der x-Achse bestimmen. Dies macht man mit der Gleichung f(x)=0. Man kann aber auch Ebenen schneiden. Wenn sich zwei Ebenen schneiden, dann hat man keinen Schnittpunkt mehr sondern eine Gerade. Eine Gerade ist aber auch ein Raum. Dieser Raum hat zwar nur eine Dimensionen (es gibt nur eine Richtung), es ist aber dennoch ein Raum. Ebenso ist ein Punkt ein 0-dimensionaler Raum. Man kann auch zwei Würfel schneiden und die Schnittfläche wäre dann ein zweidimensionaler Raum. Bei komplizierteren Gleichungen können nun auch Lösungsräume mit noch mehr Dimensionen enstehen. Ein Anti-de-Sitter Raum ist nun eine mögliche Lösung der Einsteinschen Feldgleichungen. Das heißt es ist einfach mal ein Raum der sich nach den Gesetzten der ART verhält. Dieser Raum hat zwar einige entscheidende Unterschiede zu unserer Raumzeit, aber das soll uns erst einmal nicht interessieren.

Eine Yang-Mills Eichtheorie wiederum, ist ein mathematische Theorie mit der man die starke Wechselwirkung und elektroschwache Wechselwirkung (Verbindung der schwachen Wechselwirkung mit der elektromagnetischen Kraft) in der QM beschreibt.

Dualität bedeutet nun, dass man das eine in das andere "übersetzen" kann. Das einfachste Beispiel wäre das Komplement in der Mengenlehre. Komplement ist quasi das Gegenteil. Ein einfaches Beispiel wäre das Komplement der gerade Zahlen, das sind dann die ungeraden Zahlen. Man kann hier quasi Übersetzen: Nicht die geraden Zahlen -> die ungeraden Zahlen. Nicht die ungeraden Zahlen -> die geraden Zahlen. Gerade und ungerade Zahlen sind (in der Menge der natürlichen Zahlen) dual zueinander. Es reicht einfach sich Dualität als (meistens eindeutige) Übersetzung vorzustellen.

Ist nun ein wenig klarer was Maldacena hier vollbracht hat? Er hat es geschafft quasi einen Teil der Relativitätstheorie in die Quantenmechanik zu "übersetzen". Ok eigentlich nicht wirklich, weil man im Standardmodell die SU(N) mit N=3 für die Beschreibung der starken Wechselwirkung und SU(2)xU(1) für die elektroschwache Wechselwirkung verwendet und Maldacenas Beweis nur für "sehr große N" gilt. Außerdem ist die Eichtheorie die Maldacena verwendet supersymmetrisch, während bei der Eichtheorie im Standardmodell spontane Symmetriebrüche auftreten usw. Also eigentlich passt diese Eichtheorie mal gar nicht.


Dennoch ist das Ergebnis von großer Bedeutung denn auch wenn diese Eichtheorie so nicht eingesetzt wird, ist es dennoch eine Konforme Quantenfeldtheorie. Außerdem ist die AdS/CFT Korrespondenz ein Spezialfall des holografischen Prinzips und ist somit der erste Hinweiß, dass es sich allgemein beweisen lässt. Man hat mittlerweile noch andere Spezialfälle gezeigt, was hoffen lässt, dass das ein allgemeiner Beweis möglich ist. Und es gibt noch andere Gründe zur Hoffnung...

2.5 Quark-Glonen-Plasma

unteilbar?!

Wir haben uns seit Bekenstein nur auf theoretischem Grund bewegt. Wir wollen nun aber auch mal ein Auge auf eine Erkenntnis aus der Praxis werfen. Atom kommt vom griechischen ἄτομος (a-tomos) und heißt unteilbar. Dafür, dass Atome nicht unteilbar sind, gibt es ziemlich beeindruckende Belege (Ein Beispiel dafür sieht man rechts). Atome setzen sich aus Protonen, Neutronen und Elektronen zusammen. Nun sind aber Protonen und Neutronen auch nicht unteilbar.

Proton
(Quelle: wiki)

Protonen und Neutronen bestehen aus Quarks und werden durch Gluonen (von englisch glue = kleben) zusammengehalten. Ein Proton besteht aus zwei up-quarks und einem down-quark (vgl. links). Kurz nach dem Urknall war das Universum aber so dermaßen heiß (mehrer Billionen °C) , dass die Teilchen nicht zusammenhalten konnten. Diesen Zustand versucht man mit Teilchenbeschleuniger zu reproduzieren um ihn genauer untersuchen zu können. Dafür schießt man schwere Ionen aufeinander (am RHIC nimmt man Gold, am LHC des CERN nimmt man Blei - die Amis pulverisieren Gold während die Schweizer sparsamer sind ;-) ).




Eigentlich hätte man von der QM her erwartet, dass sich das Quark-Gluonen-Plasma wie ein Gas verhält und die Teilchen gänzlich frei umher fliegen. 2005 verkündete aber das RHIC, dass sich das Quark-Gluonen-Plasma wie eine Flüssigkeit verhält. Siehe dazu auch die Publikation "Experimental and Theoretical Challenges in the Search for the Quark Gluon Plasma" der STAR collaboration (STAR ist einer der RHIC Detektoren).


Aus den gewonnen Daten hat man nun versucht die Viskosität $\eta$ (das Maß für die Zähigkeit einer Flüssigkeit - Honig hat eine höhere Viskosität als Wassser) zu bestimmen. Genauer die Scherviskosität in Abhängkeit zur Entropie ($\frac {\eta}{S}$ - ein Maß für die innere Reibung). Das ist kein leichtes Unterfangen, da sich die Dynamik von Flüssigkeiten nicht so einfach berechnen lässt und man muss dazu Simulationen machen um $\frac {\eta}{S}$ aus dem beobachteten "wabern" zu bestimmen. Außerdem hat man noch eine Messungenauigkeit aus den gesammelten Daten. Einen Vergleich der Messdaten mit simulierten Werten sieht man in diesem Schaubild:

Simulation und Daten der Scherviskosität zur Entropie
(Quelle: arXiv:0804.4015v4 )

Die bunten Kurven in obiger Grafik sind die simulierten Ergebnise für je einen Wert von $\frac {\eta}{S}$. Oben nach dem "Glauber", unten nach dem "CGC" Model simuliert. Die Punkte bzw. schwarzen Balken sind die Messwerte aus dem STAR (rechts) und dem PHOBOS (links) Detektor des RHIC. Die Balken sind dabei die Ungenauigkeiten die sich aus den Messungen ergeben. Je nach Simulation kommt man auf einen Wert von ca. $\frac {\eta}{S} \approx 0{,}08 - 0{,}16$. Hierbei ist zu beachten, dass dieser Wert in natürlichen Einheiten angegeben wird. Das macht man schlicht aus dem Grund, dass es einfacher zu Rechnen ist. Um das Ergebnis in SI-Einheiten zu bekommen müsste man noch mit $\frac{\hbar}{k_B} \approx 0{,}000000000007 {\rm \frac{K}{s}}$ durchmultiplizieren.


Es ist nun nicht nur überraschend, dass das Quark-Gluonen-Plasma eine Flüssigkeit ist, sondern auch, dass es verdammt flüssig ist (sehr niedrige Viskosität). Es ist quasi "die perfekte Flüssigkeit". Übrigens ist es dennoch als großer Erfolg der Quantenmechanik zu verbuchen, dass man das Quark-Gluonen Plasma überhaupt gefunden hat, auch wenn seine Eigenschaften erst einmal unerwartet sind. Man kann also deswegen nicht sagen, dass die QM deswegen "falsch" ist, aber so ganz richtig ist sie eben auch nicht.


Nun gab es aber eine noch viel größere Überaschung zum verhalten des Quark-Gluonen-Plasmas. Mit der AdS/CFT Korrespondenz lässt sich das Verhalten erklären...



Hierzu werfen wir einen Blick auf die Publikation "Viscosity in Strongly Interacting Quantum Field Theories from Black Hole Physics" von Kovtun, Son und Starinets. Vereinfacht formuliert hat man im Rahmen der Stringtheorie untersucht, wie sich Gravitationswellen verhalten, wenn sie auf ein schwarzes Loch treffen. Also eine reine Untersuchung von Gravitation. Das hat man dann in die "fast Quantenmechanik" also in die Eichtheorie mit den anderen Parametern (große N statt N=3) übersetzt und kam dabei auf eine untere Grenze für $\frac {\eta}{S}$ . Dabei hat man überraschender weise festgestellt, dass dies nicht nur für den von Maldacena bewiesen Fall sondern für alle bekannten Dualität von Gravitation und konformer Feldtheorie gilt:

$$\frac {\eta}{S} = \frac{\hbar}{4 \pi k_B}$$

Lassen wir den Faktor $\frac{\hbar}{k_B}$ wie oben weg (also geben es in "natürlichen Einheiten") an, dann gilt: $\frac {\eta}{S} = \frac{1}{4 \pi }$. Nicht nur, dass es überraschend ist, dass das in allen Dualität gilt, es passt auch noch auf die experimentellen Werten des Quark-Gluonen-Plasmas, denn $\frac{1}{4 \pi } \approx 0{,}08$.

(Quelle: icanhascheezburger.com)

Seit Bekenstein haben wir uns nur in theoretischen "Spinnereien" bewegt. Viele Entwicklungen in der Stringtheorie hatten eigentlich nichts mehr mit praktischer Physik zu tun und waren nur mathematische Modelle mit denen man "rumgespielt" hat. Auch die AdS/CFT Korrespondenz war in aller erster Linie nur mal eine mathematische Kuriosität (wenn auch eine sehr interessante). Und plötzlich liefern diese mathematischen "Spinnereien" experimentelle Vorhersagen. Es wäre prinzipiell möglich, dass es sich nur um einen Zufall handelt, aber es wäre absoluter Blödsinn das einfach als einen solchen abzutun und das holografische Prinzip nicht weiter zu verfolgen.


Neuere Ergebnisse vom CERN legen übrigens nahe, dass sich das Quark-Gluonen-Plasma auch bei höheren Temperaturen noch wie eine (perfekte) Flüssigkeit verhält (vgl. ALICE Collaboration "Elliptic flow of charged particles in Pb-Pb collisions at 2.76 TeV")


Aber was ist denn nun mit Einsteins zersausten Haaren und der Gravitation? Entropie (Teil I) und das holografische Prinzip (dieser Teil) haben wir schon einmal geschafft. Zur "entropic gravity" von Verlinde kommen wir dann in Teil III ...





Ergänzung:

Fast hätte ich es vergessen. Kleine schwarze Löcher im CERN? Auch eine Vorhersage der AdS/CFT Korrespondenz und diese sollten nach Hawking verstrahlen. ABER DAS IST DOCH ALLES NUR THEORIE, WAS WENN SIE NICHT ZERSTRAHLEN UND DIE ERDE "AUFFRESSEN"?

Klar ist das alles Theorie. Aber es gibt ein experimtellen Beleg dafür, dass das nicht passieren kann. Es gibt nämlich diesen riesen Teilchenbeschleuniger am Himmel genannt SONNE und dieser Beschleuniger stellt den LHC am CERN in den Schatten, denn er erreicht unvorstellbar höhere Energien. Und dieser "Teilchenbeschleuniger" SONNE bombardiert den Detektor "ERDE" schon seit verdammt langer Zeit mit Teilchen. Da ich gerade diesen Artikel auf dem Detektor ERDE schreibe und keine komprimierte Materie in einem schwarzen Loch bin, gibt es nur zwei Möglichkeiten. Entweder die Löcher entstehen gar nicht erst, oder sie zerstrahlen wirklich. Alles andere ist bei ein paar Hundert schwarzen Löchern pro Jahr und einer "Messdauer" von mehreren Milliarden Jahren ausgeschlossen. Die Angst vor diesen schwarzen Löchern ist so berechtigt wie die Angst, dass es einem im Zug die Organe zersetzt.



Siehe auch "Entropic gravity" Ergänzung zu TEIL 2: Details und ein Experiment zum holografischen Prinzip.

Zusätzliches Infomaterial 

(englisch/populärwissenschaftlich)

• Juan Maldacene in "Scientific American", November 2005: "The Illusion of gravity"
• Jacob Bekenstein in Scientific American, August 2003: "Information in the Holographic Universe"
• Symmetrybreaking: "A first: String theory predicts an experimental result"
• Marianne Freiberger in Plusmagazine Issue 51a: "The illusory Universe"