Saubere wissenschaftliche Arbeit kommt um eine Fehleranalyse nicht herum. Zwei Artikel, die ich neulich gelesen habe, sind exemplarische Beispiele, wie wichtig eine Fehleranalyse ist. Andernfalls könnte man der Meinung sein, dass tote Lachse Emotionen empfinden oder dass sich Neutrinos mit Überlichtgeschwindigkeit bewegen...
Es gibt zwei Arten von Fehlern: zufällige Fehler und systematische Fehler.
1. Zufällige Fehler
Zufällige Fehler, sind die Fehler die durch Schwankungen in einer Messreihe entstehen. Werfen wir 10 mal eine Münze und erhalten 6 mal "Kopf" und 4 mal "Zahl" so erscheint die Wahrscheinlichkeit, dass wir "Kopf" erhalten 60%. Handelt es sich um einen idealen Münzwurf, sollte die Wahrscheinlichkeit aber 50% sein. Damit man absolut sicher 50% erhält, müsste man unendlich viele Münzwürfe mit einer idealen Münze machen. Diese Abweichung, bei den zehn Würfen ist ein zufälliger Fehler.
Um nun mit einer begrenzten Anzahl von Messungen ein sinnvolles Ergebnis zu erhalten, kommt man um Statistik nicht herum. Hier spielt die gaußsche Glockenkurve eine große Rolle:
Es gibt zwei Arten von Fehlern: zufällige Fehler und systematische Fehler.
1. Zufällige Fehler
Zufällige Fehler, sind die Fehler die durch Schwankungen in einer Messreihe entstehen. Werfen wir 10 mal eine Münze und erhalten 6 mal "Kopf" und 4 mal "Zahl" so erscheint die Wahrscheinlichkeit, dass wir "Kopf" erhalten 60%. Handelt es sich um einen idealen Münzwurf, sollte die Wahrscheinlichkeit aber 50% sein. Damit man absolut sicher 50% erhält, müsste man unendlich viele Münzwürfe mit einer idealen Münze machen. Diese Abweichung, bei den zehn Würfen ist ein zufälliger Fehler.
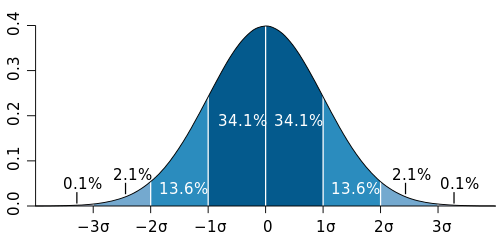
Um nun mit einer begrenzten Anzahl von Messungen ein sinnvolles Ergebnis zu erhalten, kommt man um Statistik nicht herum. Hier spielt die gaußsche Glockenkurve eine große Rolle:
 |
| (Quelle: wikipedia) |
Im Falle des Münzwurfs haben wir eine Binomialverteilung, was das Rechnen stark vereinfacht. Nehmen wir also nochmal das Beispiel mit den 10 Würfen einer idealen Münze. Bei 10 Würfen ist der Erwartungswert $\mu = \rm{n \cdot p}$ (n ist die Anzahl der Würfe (also 10) und p die Wahrscheinlichkeit mit der "Kopf" (bzw. "Zahl") auftritt). Also ist $\mu = 10 \cdot 0{,}5 = 5$. Wir sollten also bei den 10 Würfen 5 mal "Kopf" und 5 mal "Zahl" erhalten. Die Frage ist nun, welche Abweichungen zu erwarten sind. Dazu berechnet man die Standardabweichung durch die Varianz. Es gilt $\rm{\sigma = \sqrt{n \cdot p \cdot (1-p)} = \sqrt{ 10 \cdot 0{,}5 \cdot (1-0{,}5)} \approx 1{,}6}$. Was heißt das jetzt? Ein Blick auf obiges Schaubild macht das klar. 68,2% aller Fälle liegen im dunkelblauen Bereich zwischen $-1\sigma$ und $1\sigma$, also 68,2% aller 10 Münzwürfe weichen von 5 mal "Kopf" um höchstens 1,6 ab.
Die Standardabweichung kann man als ein Kriterium für ein "korrektes" Ergebnis nehmen. Messergebnisse außerhalb eines gewählten Bereichs behandelt man als Ausreißer. Die Frage ist aber, wo man die Grenze zieht. $1\sigma$? $2\sigma$? Bei $2\sigma$ würde man immerhin schon 95,4 % aller Fälle abdecken. Haben wir schon wissenschaftlicher Signifikanz, wenn weniger als 5% der Messergebnisse als Ausreißer betrachtet werden?
Hierzu mal ein Beispiel: A 3.8-Sigma Anomaly
14 Mal in Folge hat das Team der NFC beim Münzwurf gewonnen. Bei 13 Würfen wäre der Erwartungswert $\mu = n \cdot p = 13 \cdot 0{,}5 = 6{,}5$. Man kann also 6 oder 7 mal "Kopf" bzw. "Zahl" erwarten. Die Standardabweichung wäre: $\rm{\sigma = \sqrt{n \cdot p \cdot (1-p)} = \sqrt{ 13 \cdot 0{,}5 \cdot (1-0{,}5)} \approx 1{,}8}$. Wenn 13 mal das selbe kommt, weicht das von den 6,5 Mittelwert um 6,5 ab. $ \frac{6{,}5}{1{,}8} \approx 3{,}6\sigma$ (Anmerkung: Die 3,8 $\sigma$ aus dem Artikel sind fälschlicherweise mit p=14 gerechnet).
Der Autor schreibt:
"That’s a better than 3.8-sigma effect! Enough to call a press conference, if this were particle physics."
Auch wenn es bei n=13 "nur" 3,6 und nicht 3,8 $\sigma$ sind, hat der Autor Recht, dass das schon für eine Pressekonferenz reichen dürfte (zumindest als vorläufiges Ergebnis). Damit ein Ergebnis aber wirklich anerkannt wird, erwarten Teilchenphysiker eher 5 bis 6 $\sigma$. Dieses Beispiel zeigt deutlich, dass man statistische Fehler nicht unterschätzen darf. Aber kommen wir zu den Emotionen toter Lachse ...
 |
| (Quelle: Spiegel) |
"Der wohl ungewöhnlichste Proband, dessen Gehirntätigkeit Craig Bennett jemals untersucht hat, war ein toter Lachs. Seinem leblosen Versuchsobjekt stellte der Neuropsychologe von der University of California in Santa Barbara eine knifflige Aufgabe: Das fast zwei Kilo schwere Tier sollte Bilder von fröhlichen, ängstlichen oder wütenden Menschen betrachten. Währenddessen maß Bennett seine Hirnaktivität." (Quelle: Spiegel)
Der wirklich lesenswerte Spiegel Artikel "Großhirn-Voodoo" umreißt die Probleme der statistischen Auswertung recht ordentlich. Ich möchte aber an dieser Stelle einen etwas detaillierteren Blick auf das Problem werfen. Hierzu die Publikation:
Bennett et al. - Neural Correlates of Interspecies Perspective Taking in the Post-Mortem Atlantic Salmon: An Argument For Proper Multiple Comparisons Correction
Für die "multiple comparsion correction" können wir nochmal auf unser Münzwurfbeispiel zurückgreifen. Nehmen wir an, wir wollen zeigen, dass eine Münze nicht fair ist und machen 10 Würfe. Gehen wir davon aus, dass wir mindestens 9 mal "Kopf" werfen und berechnen dazu die Wahrscheinlichkeit. Die Wahrscheinlichkeit für eine bestimmte Kombination nach den 10 Würfen ist $(\frac{1}{2})^{10}$. Es gibt insgesamt 10 Kombinationen bei denen 9 mal "Kopf" vorkommt (1. Wurf "Zahl", Rest "Kopf" / 2. Wurf "Zahl", Rest "Kopf" / 3. Wurf "Zahl", Rest "Kopf" / ...). Außerdem gibt es auch noch die Möglichkeit 10 mal "Kopf" zu werfen, was die Bedingung mindestens 9 mal "Kopf" auch erfüllt. Somit sind es insgesamt 11 Kombination. Die Wahrscheinlichkeit für mindestens 9 mal "Kopf" ist also $11 \cdot (\frac{1}{2})^{10} = 0,0107421875$. Wem 2,5 $\sigma$ genügt - und in den meisten Bereichen reichen 2 $\sigma$ - der darf nun eine Pressekonferenz einberufen, auf der er die unfaire Münze und die Messergebnisse vorstellt.
Der Knackpunkt bei Bennett ist ein wenig komplizierter. Auf das Münzwurfbeispiel übertragen haben wir es beispielsweise mit 100 Münzen zu tun, die wir alle testen sollen. Berechnen wir also die Wahrscheinlichkeit, dass bei mindestens einer Münze mindestens 9 mal "Kopf" vorkommt. Hierzu berechnet man am einfachsten zuerst die Wahrscheinlichkeit, dass bei keinem Münzwurf mindesten 9 mal "Kopf" kommt. Die Wahrscheinlichkeit für mindestens 9 mal "Kopf" lag bei $0,0107421875$. Das "Gegenereignis" hat also eine Wahrscheinlichkeit von $1-0{,}0107421875 = 0{,}9892578125$. Die Chance, dass bei der ersten Münze nicht 9 mal "Kopf" kommt ist also fast 99%. Die Chance, dass beim ersten und zweiten Wurf nicht 9 mal "Kopf" kommt ist dann $0{,}9892578125 \cdot 0{,}9892578125$. Für 100 Münzen also $0{,}9892578125^{100} = 0{,}339585292062$. Die Chance, dass wir also keine Münze als unfair deklarieren müssten, liegt gerade mal bei 34%. Mit einer Chance von 66% [SIC!] kommen wir zu dem falschen Ergebnis, dass eine der Münzen unfair ist.
In obigem Beispiel mit einer Münze wäre unsere fälschlicherweise positives Ergebnis schlicht Pech. In dem Beispiel mit den 100 Münzen ist aber das fälschlicherweise positive Ergebnis schlicht auf grobe Fehler zurückzuführen. Dieses Problem zu erkennen ist gerade mal Oberstufenniveau und um diese Fehler auszugleichen gibt es Software (Man muss also kein Mathematiker dafür sein). In Bennetts Publikation heißt es:
"Sadly, while methods for multiple comparisons correction are included in every major neuroimaging software package these techniques are not always invoked in the analysis of functional imaging data. For the year 2008 only 74% of articles in the journal NeuroImage reported results from a general linear model analysis of fMRI data that utilized multiple comparisons correction (193/260 studies). Other journals we examined were Cerebral Cortex (67.5%, 54/80 studies), Social Cognitive and Affective Neuroscience (60%, 15/25 studies), Human Brain Mapping (75.4%, 43/57 studies), and the Journal of Cognitive Neuroscience (61.8%, 42/68 studies)." (Quelle: Bennett S. 2)
Meiner Erfahrung nach ist dies kein Einzelfall sondern eher exemplarisch. Mal abgesehen davon, dass die Standards in einigen Wissenschaftsbereichen schon relativ gering sind (2$\sigma$), scheitert es nicht selten schon an der Einhaltung dieses Minimums. Und das waren bisher nur die zufälligen Fehler...
(to be continued)
Interessant. Leider habe ich oft eien Anzeige "Math Processing Error". Wie bekomme ich die weg?
AntwortenLöschenHmm, ich habe das MathJax Script auf Firefox, Konquerer, Android Stock Browser und Android Chrome Beta getestet und es funktioniert. Infos zum Browser und Version wäre hilfreich.
AntwortenLöschenIch habe gerade noch IE9 gecheckt und dort gab es ein Problem mit dem Script, da das template im IE7 Kompatibilitätsmodus lief und das script nicht ausgeführt werden konnte. Das Problem habe ich behoben. Sollte also alles funktionieren sofern der Browser "up to date" ist.
Löschen